Calques 3D : a microworld for spatial geometry learning
Abstract. Calques 3D is a microworld designed for constructing, observing and manipulating geometrical figures. It provides the user with functions and visual feedback for seeing and understanding objects in the third dimension. It also allows him to dynamically construct geometrical figures from elementary objects and construction operations and, finally, to explore and discover the properties of the figure by deforming it.
Introduction
In French secondary level schools, spatial geometry teaching is an important goal in mathematics teaching, and a difficult one, mainly because students have intrinsic difficulties in visualising three dimensional objects. Indeed, students are often unable to see and understand the display of a 3D figure on a 2D device, and then to proceed to form an abstraction of it. Moreover, though 'wire-frame' geometry does not introduce the same difficulties as solid geometry: it can cause other problems since the translucent aspect of objects makes it difficult to visualise their relative position.
Thus, the use of computers to display real-time and interactive images of 3D construction should be helpful for overcoming this problem. This observation led us to explore the field of Dynamic Geometry [Balacheff 94, Goldenberg 98]. In this context, our project could rely on similar research, both in plane geometry (e.g. Geometer's Sketchpad [Jackiw 95], Cabri-geometry [Laborde 94] or Calques 2 [Bernat 94] - the later developed in our research team), and in spatial geometry (e.g. Geospace [Authier 98], Kappa [Muzellec 96] ou Cabri 3D [Qasem 97]).
Calques 3D is a microworld, i.e. a type of Interactive Learning Environment (ILE), designed for constructing, observing and manipulating geometrical figures. It allows an intuitive and adaptable access to environment features. Intuitive because it is used by students who do not have preparation. Adaptable because it allows the teacher to decide, with respect to his own pedagogy, which primitives and operations will be made available to the student. The aims of Calques 3D are threefold :
- Observation: allowing one to see and understand the third dimension by changing the spatial system of reference (axes, floor, etc.), choosing perspective ('cavalière', vanishing point, etc.), modifying the observer's point of view; displaying visual feedback on objects, etc.
- Construction: allowing a dynamic construction of geometrical figures from elementary objects (points, lines, planes, etc.) and construction primitives (intersection, parallel, perpendicular, etc.).
- Exploration: allowing one to explore and discover geometrical properties of the figure (deforming it by directly dragging base-points, changing observer's point of view, etc.).
Observation of figures
Calques 3D provides the student with support for helping them visualise geometric objects and moving from a concrete to an abstract environment. The student can observe a geometrical construction from various angles by modifying the observer's point of view or by requesting a frontal point of view for 'real-sized' observation.
The choice of a spatial system of reference can influence the visual presentation of geometrical objects. For example, the 'dividing walls' and the 'floor' can be used for representing the points co-ordinates by their projection on each wall. This also allows one to display their intersections with geometrical objects like lines, circles, planes, etc. and, in the same way, to display those parts which are 'visible' or not, i.e. changing the drawing features (e.g. line thickness) or the colour of object part behind the walls or under the floor (Fig. 1).
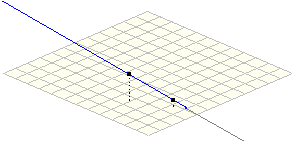
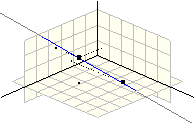
Figure 1. Using the spatial system of reference for concrete representation of a line's intersections with the 'floor' (left) or the 'dividing walls' (right).
Every geometrical object introduces different types of visual units for comprehension : the normal vector for planes or circle, etc. In order to obtain a suitably balanced marriage between visual help and visual overload, they could appear either automatically when the corresponding object is in use (e.g. during its creation, its designation in a construction task or during figure deformation if the target object is a movable point) or from an explicit student's request (e.g. by marking expected objects and switching on/off the marks).
Construction of figures
Calques 3D allows the student to create figures of spatial geometry by constructing elementary geometrical objects (e.g. lines, segments, planes, spheres, etc.) and by establishing geometrical relationships between them with construction primitives (e.g. parallel, perpendicular, membership, intersection, etc.). At each step of the construction task, contextual help and visual feedback provide the student with immediate and useful information about the current state of the task and about the stages remaining to complete it.
For ergonomic reasons, the construction task could be quite different from the 'traditional' one, for example in cube construction. The first step of this construction consists in designating two distinct points which provide the initial edge of the cube (Fig. 2).
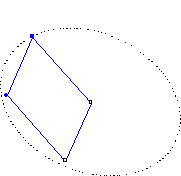
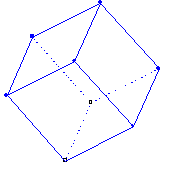
Figure 2. The three steps of the creation of a cube: the first edge designation (left), the first face creation and orientation (middle) and the final cube extension (right).
Once the second edge extremity is selected, a circle, in a perpendicular plane to this edge, centred to the second extremity and with a radius equal to the edge length, is drawn. The first cube face and its orientation around the edge can then be defined by creating and dragging a point on this circle. Finally, the cube itself is obtained by extending it from the face either in an arbitrary direction or according to the user's choice. In this way, during each creation step, it is possible to provide visual feedback that allows the user to focus on what he is currently creating.
Exploration of figures
The plane representation of a spatial figure (i.e. the drawing of the figure [Parzysz 88]) does not sufficiently allow the student to understand all its geometrical properties, even if he could modify the observer's point of view. The dynamic deformation of such a figure provides the user with another way for exploring them. The exploration of figures is realised through an interface based on an extension of the direct manipulation concept [Schneiderman 82, Nanard 90] for spatial environments. Because of the limitations of user-interfaces for 3D manipulation, Calques 3D applies what we call 'the geometry of the point' : the deformation of a construction can be accomplished only by dragging movable points (e.g. by segment extremities). Other geometrical objects can not be accessed (e.g. by any point of the segment).
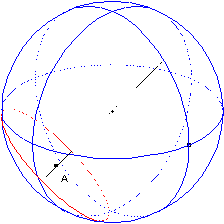
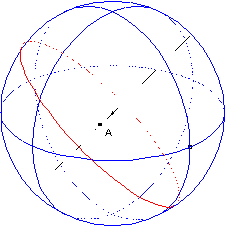
Figure 3. Evolution of the plane section of a sphere during the deformation (translation of the point A along a radius of the sphere).
During the point dragging (Fig. 3), Calques 3D maintains the coherence of the relations either explicitly specified in the figure or resulting from the construction, and calculates and redraws in real-time the new shape of the construction.
The tracings: a feature of Calques 3D
We define a tracing as a visual filter, i.e. a mechanism that allows the user to extract from the construction a subset of geometrical objects and to visualise them separately from the initial figure. A subset of the figure is a set of defined geometrical objects taken as a whole (lines, points, planes, etc.) : it is impossible for example to extract a part of a line, a half-plane or a half-sphere, or the plane section of a cube if this locus was not explicitly constructed.
As a visual filter, the tracings objective is only used to ease the observation of a part of the construction : it consists in sharing an objects' visual representation with independent views that can be shown at the same time. These views (called 'Tracing Views') are similar to the main construction view (called 'Universe View'), i.e. it allows the user to change the observer's point of view, the spatial system of reference, the zoom factor, etc. in each of the views but the visual attributes of extracted objects are shared among them. Moreover, the construction of new objects is not allowed in a tracing window.
The tracings could be used to overcome the loss of spatial information, when drawing on a 2D screen, by simultaneous visualisation of different points of view of the same figure (or on some of its parts). For example in Fig. 4, a cube could be displayed in the 'Universe View' with one point of view while a triangle, filtered of one of its face, could be displayed in another window with another point of view (e.g. a frontal point of view, such that the triangle appears as 'real-sized'). In some ways, the tracings are similar to the 'front view', 'rear view' and so on that come from technical drawing.
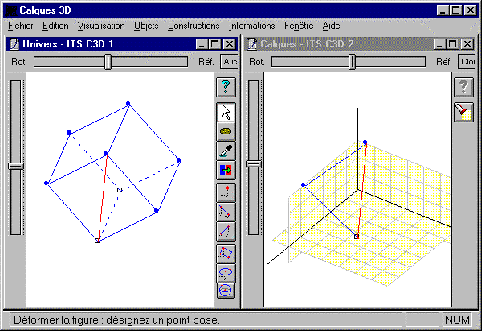
Figure 4. A snapshot of Calques 3D main window; at left, a cube in the 'Universe' window; at right, a triangle extracted from one of its face and visualised in a separate 'Tracing' window.
The dynamic features of the microworld introduce some new properties that can be useful for more easily observing a figure. Indeed, the geometrical relations that link objects in the construction are not lost during the extraction process : any deformation that is made in one view results in a similar deformation in all the other views. That is why we consider the tracings as a visual filter rather than as a copy-and-paste tool.
Conclusion
Calques 3D is a prototype still being developed. We have shared it with eight teachers, who are collaborating with us. They are currently evaluating it and providing us feedback. This microworld provides users with a minimum but sufficient set of operations for the construction and the observation of geometrical figures. The prototype will be upgraded in order to take into account other teachers' needs. It should be notes that, Calques 3D only supports 'wire-frame' geometry: it does not allow the users to practice solid or analytical geometry. Calques 3D was developed with Borland C++ 4.5 (about 25000 code lines) and is available for PC 486 systems or higher. It requires Windows 3.1 or Windows 95/NT.
References
Authier, A., Grolleau, C., Hocquenghem, M.L., Hocquenghem, S., Monnet, F., Paquelier, Y., Sérès, P., Serfati, A.M. and Varoquaux, A. (1998). Géospace : logiciel de construction mathématique dans l'espace, CREEM (CNAM) - CRDP de Champagne-Ardenne.
Balacheff, N. (1994). Didactique et intelligence artificielle. In Didactique et intelligence artificielle. N. Balacheff et al. Grenoble, La Pensée Sauvage.
Bernat, P. (1994). Calques 2. Pont-à-Mousson, Topiques Editions.
Goldenberg, E.P. and Cuoco, A. (1998). What Is Dynamic Geometry? In Designing Learning Environments for Developing Understanding of Geometry and Space. R. Lehrer et al. Hillsdale, NJ, Erlbaum.
Jackiw, N. (1995). The Geometer's Sketchpad, Visual Geometry Project, Key curriculum Press.
Laborde, J.M. and Bellemain, F. (1994). Cabri-Géométre II, logiciel et manuel d'utilisation. Dallas, TX, Texas Instruments.
Muzellec, D. (1996). Le logiciel KAPPA, la géométrie en trois dimensions. Cari-info. Académies de Nantes: 10-11.
Nanard, J., La manipulation directe en interface homme-machine. Ph. D. Thesis. Université de Sciences et Technique du Languedoc, Montpellier II, (1990).
Parzysz, B. (1988). Knowing vs. Seeing, problems of the plane representation of space geometry figures. Educational Studies in Mathematics 19(1): 79-92.
Qasem, S. (1997). La représentation dans un micro-monde de géométrie dans l'espace : le cas de Cabri 3D. EIAO'97 - Cinquièmes Journées EAIO de Cachan, HERMES, Paris.
Schneiderman, B. (1982). The future of interactive systems and the emergence of direct manipulation. Behavior and Information Technology, 7: 237-256.